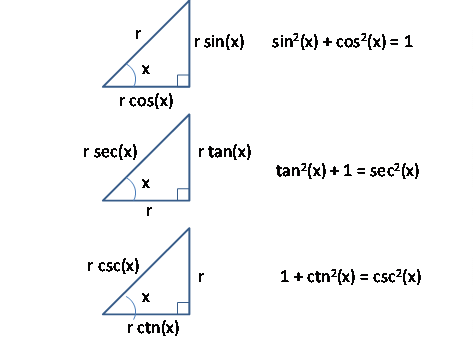Trigonometric Functions

 

INTRODUCTION

 

We start with an arbitrary right triangle shown below.  What is most important is its shape and not its size.  By shape we mean that we know what all the angles are.  And if we know the shape, then we know what the various ratios of all the sides are.  That is because the ratio of any two sides is a constant and does not depend on the absolute values of the lengths but only on the angle between them.

 

 

 

 

 

 

 

 

 

 

 

 

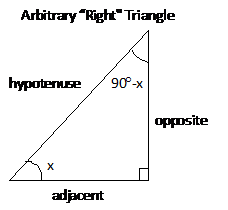The advantage of all of this is that if we measure one length and one angle “x” as shown above, then we can calculate the other two lengths.  In the following equations, the names “hypotenuse”, “adjacent”, and “opposite” are abbreviated as “hyp”, “adj”, and “opp”.

 

TRIGONOMETRIC FUNCTIONS

 

Since a triangle has three sides, there are six possible ratios of any two sides.   Each ratio is given a name and represents a particular trigonometric function. 

 

 

 

 

 

 

 

Note that in practice, the first three functions, {sine, cosine, and tangent}, are by far the most important.  The functions {secant and cosecant} are hardly ever used.

 

PYTHAGOREAN THEOREM

 

As previously mentioned, if we know one angle “x” and the length of one side “r”, then we can easily compute the lengths of the other two sides.  The various combinations are shown below.  In addition we can use the Pythagorean Theorem to derive further relations between the various trigonometric functions.