Trigonometric Formulas
INTRODUCTION
Trigonometry is the study of triangles and especially right triangles. Central to this endeavor are the sine and cosine of the sum of two angles. These two formulas can then be used to derive all the other trigonometry formulas for some twenty in total.
SINE AND COSINE OF THE SUM OF TWO ANGLES
To start we first draw two
right triangles, ![]() with an angle of
with an angle of ![]() . We then draw the lines
. We then draw the lines ![]() and
and ![]() to create the right triangle
to create the right triangle ![]() , which also
contains the angle
, which also
contains the angle ![]() .
.

Please recall that if we know the hypotenuse “r” and one other angle “x” of a right triangle, then we can calculate lengths of the other two sides as follows
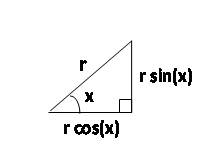
Considering the triangle ![]() we can write
we can write
![]()
And finally rearranging
![]()
Again considering the
triangle ![]() , we can write
, we can write
![]()
And so rearranging
![]()
SINE AND COSINE OF THE DIFFERENCE OF TWO ANGLES
From simple geometric considerations we can write
![]()
![]()
These allow us to write the formulas for the difference between two angles as
![]()
![]()
TANGENT OF THE SUM AND DIFFERENCE OF TWO ANGLES
For the tangent, we can write
![]()
so that we can write
![]()
by
dividing the top and bottom by ![]() , we get
, we get
![]()
And likewise by noting
![]()
we get the result
![]()
DOUGLE ANGLE FORMULAS
If we set ![]() , then using the formula above we can write
, then using the formula above we can write
![]()
From the Pythagorean Theorem for the above triangle with r=1, we can write
![]()
Combining these two gives us
![]()
In like manner we can write the double angle sine formula as
![]()
or
![]()
And for the tangent we can write
![]()
or
by dividing top and bottom by ![]() we can write
we can write
![]()
HALF ANGLE FORMULAS
If we set ![]() , then by recalling the relationship
, then by recalling the relationship
![]()
we can write
![]()
![]()
And from the relationship
![]()
we can write
![]()
TRIGONOMETRIC SUMS AS PRODUCTS
If we set ![]() and
and ![]() , then we can rewrite our original angles as
, then we can rewrite our original angles as
![]()
![]()
and substituting these into the formulas for the cosine of the sum and difference of two angles
![]()
![]()
And by adding and subtracting these two equations, we have
![]()
![]()
And using the formulas for the sine of the sum and difference of two angles
![]()
![]()
And by adding and subtracting these two equations, we have
![]()
![]()
TRIGONOMETRIC PRODUCTS AS SUMS
We can return to the original angles and rearrange the trigonometric sums as products on the left hand side.
![]()
![]()
![]()
![]()
FINAL NOTE
The discerning student will
note an implicit assumption in that the sum of two angles, i.e. ![]() , is less than 90 degrees. While strictly correct,
we can nevertheless use the formulas for the sine and cosine for angles greater
and than 90 degrees for all the various combinations. The final result is
exactly the same. From that point no further such assumptions need be made.
, is less than 90 degrees. While strictly correct,
we can nevertheless use the formulas for the sine and cosine for angles greater
and than 90 degrees for all the various combinations. The final result is
exactly the same. From that point no further such assumptions need be made.