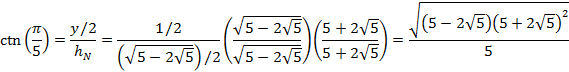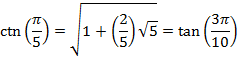The Golden Ratio

 

INTRODUCTION

 

Two lengths have a golden ratio if the smaller divided by the larger is equal to their absolute difference divided by the smaller value.  Note this is also true if the larger divided by the smaller is equal to their sum divided by the larger.  In any event, this quantity was known to the Greeks and was included in Euclid’s Elements composed roughly 300 B.C. 

 

This proportion is considered aesthetically pleasing when it appears in architecture and in nature.   Whether by design or by chance, this ratio appears in the Pantheon in Athens and the pyramids in Egypt.  Human faces, flowers, nautilus shells from the ocean, and the spiral twist of hurricanes and galaxies also exhibit this ratio.  This ratio is also closely related to the Fibonacci series in which the ratio of adjacent elements approaches the Golden Ratio as a limit.

 

GEOMETRIC RATIOS

 

A geometric approach to calculating this ratio is to start with an isosceles triangle ABC with two equal sides of length “y” and a base of “x” as depicted below.  An additional motivation for this exercise is that it provides, like only a few other triangles, a way to calculate the trigonometric functions for a specific angle, e.g. {0°, 30°, 45°, 60°, 90°}.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

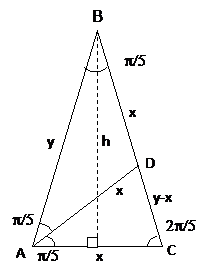Note that the figure ABC is an isosceles triangle with two equal sides of length “y” and a base of “x”.  And because the triangles ABC, ADC, ABD are all isosceles then

 

 

And because the triangles ABC and ADC are similar, i.e. have the same shape, we can write an equation for the ratio of their sides as

 

 

In both cases applying the quadratic formula gives us a solution for the golden ratio “”

 

 

And the inverse is

 

We may also write the self-referring relationship that

 

 

Returning to the diagram above, the height of the triangle is

 

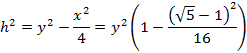
or

 

 

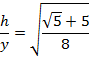
EXACT VALUES OF TRIGONOMETRIC FUNCTIONS

 

We can then derive exact values for the trigonometric functions for an angle of

 

 

 

 

 

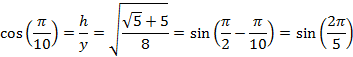
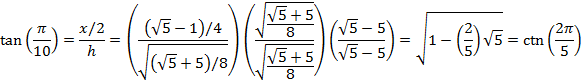
We can redraw part of the triangle ABD above and add a line AE perpendicular to the line AB as follows

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

where

 

or

 

 

The trigonometric functions for an angle of  are then
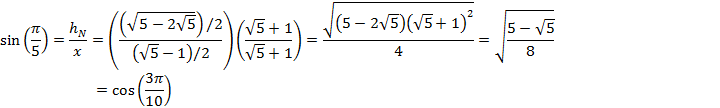