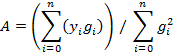Non-Linear Curve Fits

 

 

INTRODUCTION

 

Frequently we have a table of values as a function of a single variable which may have measurement noise or other inaccuracies.   These would be of the form

 

 

What we want to do then is to find the “m” parameters “λ” of some function f(x; λ) which is “non-linear” in the parameters and provides the best fit to the tabulated data.

 

 

NON-LINEAR FITS

 

Given some function, then at each data point we can write

 

 

for the “m” parameters   

 

and where “” represents the uncertainty or measurement error  as a consequence of an imperfect initial estimate of the parameters.   We can then approximate the errors as a linear combination of corrections to our parameter set as

 

 

where  which could be used to iteratively update the original set as

 

 

 

 

Writing out the entire matrix we get

 

 

or more concisely

 

 

But this is an over determined set of equations and not in form allowing for a unique determination of the parameter corrections,  .   So we multiply each side by the transpose of the matrix “A” which switches rows and columns as

 

 

So that

 

 

where

           

 

and for each element

 

 

And also by recalling

 

 

then

 

 

or finally

 

 

which allows for a unique solution for  values.

 

 

GAUSSIAN FUNCTION

 

The well known Gaussian distribution (also called the “Normal” distribution or Bell curve) has the general functional form

 

 

where the three parameters are given by

 

 

In this parameter set, A is area under the curve of G(x).  The arithmetic average or mean is .   And the last parameter σ is the standard distribution.   These are further described in the Appendix: Gaussian Parameters.

 

We can write the derivatives of the Gaussian with respect to its three parameters as follows

 

 

 

 

The iterative corrections to the initial guess for the three parameters can be expressed in the equation

 

 

or in detail, this expands to the following

 

 

For the measurements of

 

 

then the individual matrix coefficients are

 

 

 

 

 

 

 

And defining

 

 

then the matrix elements are

 

 

 

 

We could solve the matrix equation using Gauss-Jordan but for only three parameters it is easier to write the solutions directly as

 

 

 

 

 

 

And this allows us to iteratively update the initial guesses for the parameters

 

 

 

APPENDIX: GAUSSIAN PARAMETERS

 

For a random variable, X, perhaps with a Gaussian probability distribution, the results of “n” independent measurements can be represented as

 

 

The arithmetic average or mean of this series of “n” values is simply given by

 

 

and the variance (or square of the standard distribution) for a large number of “n” trials can be written

 

 

These equations are exact and work well for a small number of samples.  But as the number of samples increase, it is easier to create a histogram.

 

Basically the data is grouped into a set of “m” bins where “y_j” represents the number of values which lie within some small range, “Δx”, around a midpoint of “x_j”.  Each small range represents a separate bin and can be drawn as

 

 

 

As before the expression for the mean is

 

 

 

 

and the variance can be written as

 

 

 

As the number of discrete bins increases and the width “Δx” of each gets smaller, then the bins come to resemble a continuous curve as follows:

 

 

For a continuous curve the area under the Gaussian is given by

 

 

 

The mean value can then be written as

 

 

And the variance is given by

 

 

 

APPENDIX: INITIAL ESTIMATE

 

For a discrete set of data points

 

 

then if we first define

 

 

then the arithmetic average or mean value of the distribution is given by

 

 

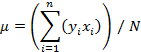
and the variance or square of the standard deviation is given by

 

 

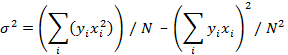
But since we are linear in A, we can write

 

 

where

 

then the total error associated with an initial guess for A is

 

 

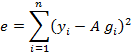
and we can minimize A in a least squares sense by setting the derivative to zero

 

 

or