MORTGAGES

 

HOW TO COMPUTE A MONTHLY MORTGAGE PAYMENT

 

If we are given the following quantities

 

            P₀ – loan amount to buy real estate or the “principal”

            r   - monthly interest rate

            n   - number of monthly payments

 

Then we can calculate the monthly payment which completely repays the loan in the last month

 

            M – monthly payment

 

At the end of each month the amount still owed on the loan changes in two ways.  In the first place, the principal, P_i for i^th month, increases as a result of interest on the loan.  And secondly, the principal is reduced an even a greater amount by the monthly payment.   This is cumulatively expressed as

 

 

and so forth until the last month when the principal is zero having been paid off, as follows

 

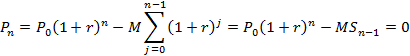
If we let  then we can solve for the summation term as

 

 

 

 

 

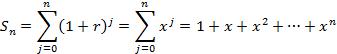
Substituting this result into the equation above gives

 

 

And we can solve directly for the required monthly payment to completely retire the loan in “n” months as

 

 

 

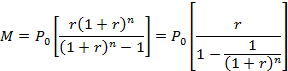
ANNUAL PERCENTAGE RATE

 

When we borrow money to buy a house, lenders charge fees “C” to originate the loan.  These fees increase the loan amount beyond the actual cost of the house “P₀” and effectively appear to the buyer as an increase in the interest rate.

 

This new interest rate is called the Annual Percentage Rate (APR) which we represent as “A”.   For convenience we will change the annual APR interest “A” to a monthly rate of “a”

 

 

To calculate the APR, we first compute the monthly payment “M_new” necessary to repay the combined amount of “” in “n” installments at the original interest rate of “r”.   This is the actual payment we will have to make.

 

 

Then for this monthly payment, we compute the effectively increased monthly APR interest rate “a” by assuming the monthly payment, which we just calculated of “M_new” was intended to repay just original principal, that is the initial cost of the real estate ”. 

 

We go to this trouble because we are confronted with a monthly payment of “M_new” and the only thing of lasting value we have for our money is the real estate.  The original interest rate “r” has been corrupted.  Legislation requires the disclosure of the APR so lenders will not be able to hide, much as they would like to, their incredibly over-inflated charges which are occasionally even for non-existent services.   And do not be fooled as these charges are negotiable and frequently reduced when challenged as they are basically insupportable.  Another common fraud is “title insurance” which, believe it or not, insures nothing.

 

 In any event the relevant equation involving the increased effective interest rate “a”, or APR, is

 

 

Unfortunately, there is no closed form solution for this equation so we have to use the Newton-Raphson approximation to solve for “a”.  This equation can be made homogeneous in the variable “a” as follows

 

 

Rearranging terms we can define the equation f(a) and calculate its derivative as follows

 

 

 

We then use successive approximations starting from an initial guess “a₀” for the APR.  For each approximation “a_i“ we use Newton-Raphson to get an even better approximations “a_i+1“ as follows

 

 

 

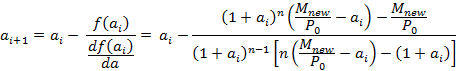
STARTING VALUE FOR THE APR CALCULATION

 

We can get an initial guess of “a₀” by considering the basic definition of APR

 

 

Then if we let   and recall that

 

 

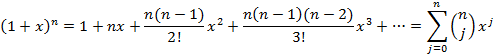
so that for

 

Then rewriting the above equation we have

 

 

And we can solve for “” as follows

 

 

Or finally, the improved starting value “a₀“ for Newton-Raphson is

 

 

Note that this is always slightly less (typically on the order of 10%) than the final value.

 

 

STABILITY OF THE “APR” CALCULATION FROM “a₀”

 

Please note that the Newton-Raphson method only converges for starting values of “a₀” which are reasonably close to the exact answer.  Please recall that the exact answer is that “a” which makes f(a) equal to zero .   In any event, Newton-Raphson requires that the slope of the curve f(a) not change sign between the initial guess and the final exact solution.   Otherwise successive approximations will diverge.   In our case the function f(a) has a local maximum where its slope is zero, that is

 

 

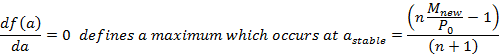
To illustrate, a plot of a specific f(a) as a function of “a” is given below

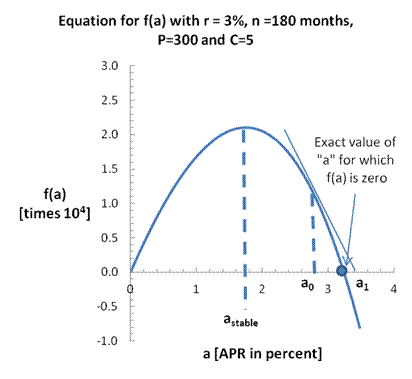
It should be obvious that if the initial guess of “a₀”, is smaller than “a_stable”, repeated applications of the Newton-Raphson” iteration will give negative values and will not approach the exact value for “a”.   But if “a₀” is large enough so that “a₀ > a_stable”, then | f(a)-f(a_i) | can be made as small as one wishes as i -> ∞.

 

The question arises as to whether the above estimate for the starting value “a₀” is stable, which means

 

 

This can be further reduced to

 

 

And continuing

 

 

But we note from the binominal expansion by expanding the first few terms

 

 

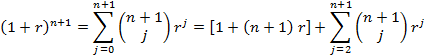
And that

 

 

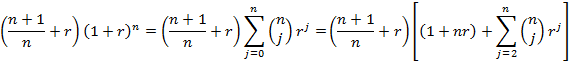
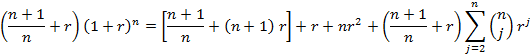
So that the equality reduces to

 

 

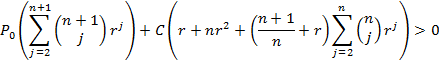
which for positive values of P₀, C, n, and r is, by observation, always true.  And so we note the starting value given above is always in the range of stability which is to say that “a₀ > a_stable” and so starting from “a₀” always works.