Fundamental Theorem of Trigonometry

 

INTRODUCTION

 

The fundamental assumption of trigonometry is that if a triangle, or indeed any polygon, changes its size but not its shape, then the lengths of all the edges are multiplied by exactly the same factor.  This means that if one edge doubles in length, then all edges double in length.  And so the ratio of any two sides remains the same as the figure shrinks or expands.

 

This is important and so we offer a rigorous proof rather than the typical appeal to fuzzy minded reasoning.  The proof comes from two sections of Euclid’s Elements Book VI namely Propositions 2 and 4. 

 

Euclid was a Greek mathematician who lived in Alexandria, Egypt about 300 BC.  His 13 Books provide the first logical development of geometry assuming only simple set of axioms.    As such it is one of the more influential mathematical works ever written.

 

Please recall the area “A” of any triangle is given by the formula

 

 

 

EUCLID’S CLAIM OF BOOK VI PROPOSITION 2

 

Consider a general triangle ACE of arbitrary size as shown below.   The line extended through BD is parallel to the base of the triangle AE.  Also the perpendicular distance from the point B to the line CE is h1 and from point D to AC is h2.

 

 

We can then write the areas “A” of various smaller included triangles as follows

 

 

 

 

The since A_ABD = A_EBD, we can divide each by the area of the top triangle A_BCD and set them equal as

 

 

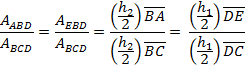
The result is that the line BD which is parallel to the base of the triangle ACE, cuts the other two sides in equal proportion as

 

 

 EUCLID’S CLAIM OF BOOK VI PROPOSITION 4

 

We next make the central claim of this exercise.  This is that if we have two “similar” triangles, but of different sizes, then the ratios of the lengths of corresponding sides are identical.   By “similar” we mean that both triangles are the same shape so that the three angles of the first triangle are the same as those in the second.

 

To prove this we first draw two similar triangles ABC and CDE which have different sizes and arrange their bases along the same straight line AE as shown below:

 

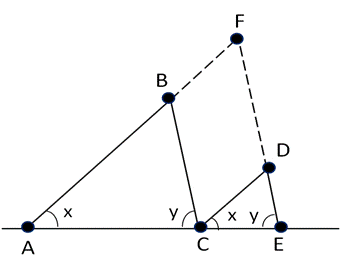
Then by extending the lines AB and ED to the point “F” we have created a parallelogram of BCDF with two sets of parallel sides which must each be of equal length.

 

Using the result of Proposition 2 above, we note that the line BC is parallel to EF.  Thus we can write

 

 

Again using Proposition 2, we note that the line CD is parallel AF.  Again we can write

 

 

We recall that any parallelogram to include BCDF has equal length sides as

 

 

 

Or combining everything, the ratios of two sides of similar but different size triangles are the same

 

 

Thus if we change the size of a triangle without changing any of its angles, then the ratio of the length of any side in the bigger triangle to the same side in the smaller triangle is exactly the same.   That is to say any expansion or contraction of the basic shape is “linear”.  And this is the fundamental assumption of trigonometry.