The Elegance of Exponents

 

 

INTRODUCTION

 

An exponent “n” can be written as follows

 

 

where the base “a” is a real number greater than zero.   If the exponent “n” is a positive natural

number then this expression simply means we multiply the base “a” by itself “n” times

 

Simple examples are

 * a

 * a * a

 

INTEGER EXPONENTS

 

If we allow the exponents “m” and “n” to be integers then we can write the relations

      or    

 

        or    

 

 

and also

 

 

 

 

FRACTIONAL EXPONENTS

 

Rational numbers “t” are those which can be expressed as a fraction.  We can express this as

 

           

 

Recall that the square root of “a”, is that number which when multiplied by itself gives a.

 

 

And using the equations above, we can write

 

 

Solving for “t” we have

 

So that

 

 

We can generalize this result to note that a^1/s is simply the “s-th” root of “a” or the number which when multiplied by itself “s” times gives “a”.

 

                       

 

 

 Or more simply we simply have the “s-th” root of “a”, as follows:

 

 

Continuing the analogy, we can use arbitrary fractions for the exponent, as given below:

 

 

or that a^{( r/s )} is the “s-th” root of the base “a” multiplied by itself “r” times.

 

And as before if the rational fraction for the exponent is negative, we can write

 

 

IRRATIONAL NUMBER EXPONENTS

 

So far we have considered rational fractions, t = (r/s), where r and s are integers and s is not zero.  There are many other numbers, however, which cannot be expressed as any rational fraction and are therefore called “irrational.”

 

The most famous irrational number is the square root of two.  Sometime around the 6^th century B.C. the Pythagorean Greeks discovered that any rational number fraction which might be equal to the square root of two had to have a numerator and a denominator both of which were infinitely divisible by two.  Since no integer has these properties, the square root of two cannot be expressed as a rational fraction.

 

Please note that all rational numbers, or fractions, when expressed as decimal numbers eventually have strings of digits that repeat forever.  Irrational numbers never have repeating sequences of digits.

 

Nevertheless for any irrational number, we can always find some rational fraction which approximates it to any degree of precision for which we have the patience.  That is to say that for any irrational number “q”, we can approximate it in the limit

 

 

Then as consequence, we can also write

 

 

One way to approximate “q” is to write it as a decimal for as many digits as are desired; and then substitute an integer divided by some power of ten.

 

For instance

                       

 

REAL NUMBER EXPONENTS

 

The rational fractions and irrational numbers together comprise the number set called the “real” numbers, .  And we have previously described exponents for both of these subsets which together constitute the entirety of the set

 

 

IMAGINARY NUMBER EXPONENTS

 

An interesting property of any real number, whether positive or negative is that if you multiply that number by itself, the result is always positive.  This means there is no “real” number that could be the square root of any negative “real” number.  This is a direct consequence of the fundamental assumption of algebra called the “Distributive Law” or

 

           

 

For a variety of calculations which are essential to the development of modern technology, we need the square roots of negative numbers.  The solution was to invent a non-physical quantity called “i” which is defined as the square root of minus one.

 

           

 

The set of all imaginary numbers, , is simply every real number, “x”, multiplied by the weird constant “i”, as follows:

 

 =

 

where  simply means “for all”.   Around 1740 A.D., Swiss mathematician Euler discovered an elegant formula describing imaginary exponents.  The starting point is to define a function using trigonometric functions and the constant “i” as follows

 

           

 

Taking the derivative with respect to x, we get

 

 

Rearranging terms and integrating both sides with respect to “x” yields

 

 

The result of the term on the left hand side is the natural logarithm, ln(z), to base “e” which is a constant approximately equal to 2.718281828…

 

 

But since

 

 

Then

 

or

 

The result is

 

 

And finally, we note the imaginary exponent has real and imaginary parts, as

 

 

This can be visualized as follows

 

 

 

Values along the “imaginary” axis are simply real numbers multiplied by “i”.  The angle x is expressed in radians.  Every point in the “complex” plane is thus some value of r*z(x) which has a real and imaginary part.    If r = 1, then every possible result for “ e^ix “ lies on the circumference of the corresponding circle.  

 

Some bizarre examples relating fundamental numbers of nature include the following

 

 

 

What exactly is the significance of these relations is still to be determined.

 

Connecting imaginary numbers with trigonometry is de Moivre’s formula when   and , then

 

 

 

Likewise we can write the trigonometric functions as

 

 

 

COMPLEX NUMBER EXPONENTS

 

A “complex” number is defined as simply the sum of a real number and an imaginary number so for

 

then simply

           

 

 

EXPONENTS USING MATRICES

 

Matrices can also be raised to powers.  For instance we might have an arbitrary matrix “A” with “m” rows and “n” columns, then

 

 

If this matrix is square, “A_{m x m}“, only then we can define a Natural number exponent “p” as follows

 

 

or in general

 

 

where the matrix “A” is simply multiplied by itself “p” times.  And for the special case

 

 

where the “Identity” matrix “I” has ones along the diagonal but zeros everywhere else.  This is not to be confused with the “Zero” matrix, Z”, which has zeros everywhere as

 

 

Also note that the inverse matrix “A^-1“ has a specifically different meaning than we might expect as follows

 

 

But a matrix can also be used as an exponent (so that “e^A “ is itself a matrix) as follows

 

 

Note that in the special case where the matrix has only diagonal non-zero elements as

 

 

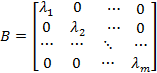
so that

 

 

APPENDIX: Infinite Number Sets

 

Please note that we will use the following symbols to represent different well-known infinite number sets.

 

                                                      - Natural or counting numbers

                                     - Integers

                         - Rational numbers

         - Real numbers

                          - Imaginary numbers

              - Complex numbers

 

where “∀” simply means “for all”, “∈” means ”is a member of the set”, and “|” means “such that”.