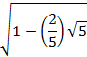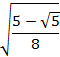Exact Trigonometric Values

 

INTRODUCTION

 

From right triangles with one base angle of {18°, 30°, 36° and 45°}, we can derive several exact values of trigonometric functions.  From this start we can apply the half angle formulas and after that we can apply sum and difference formulas.  But please note that while it is a relatively straightforward exercise to get values for angles which are multiples of 1.5° by direct application of standard formulas, other angles are extremely difficult to calculate directly.

 

SIMPLE TRIANGLES

 

The first case is an isosceles right triangle as follows:

 

 

 

 

 

 

 

 

where  a

 

 

 

The second case is an isosceles triangle divided in half as follows:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

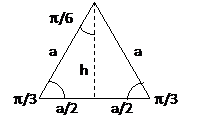BASIC TABLE OF VALUES

 

From the two triangles above and a triangle with the Golden Ratio, the table of exact values is as follows:

 

 

 

HALF ANGLE FORMULAE

 

From these basic values we can apply the following half angle trigonometric formulas to get exact values for more angles. 

 

 

 

 

 

 

 

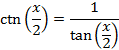
From these fundamental values we can then apply the half angle trigonometric formulae

So that for an angle of 9° or  radians

 

 

 

 

 

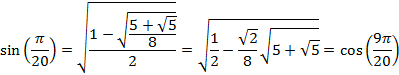
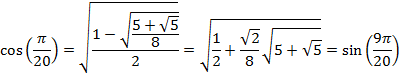
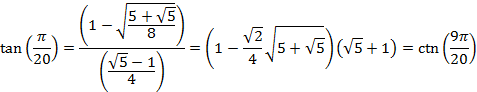
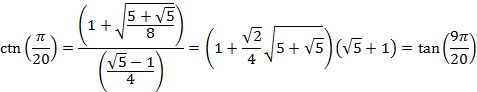
And for an angle of 15° or  radians

 

 

 

 

 

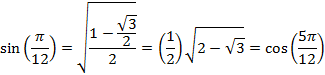
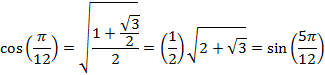
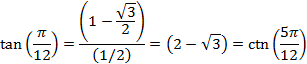
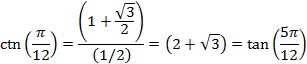
And for an angle of 22.5° or  radians

 

 

 

 

 

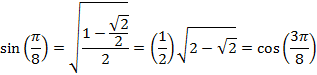
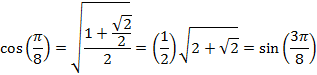
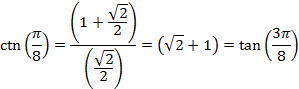
And for an angle of 27° or  radians

 

 

 

 

 

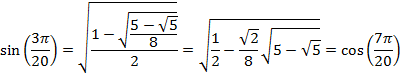
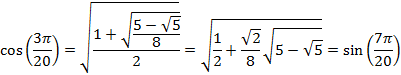
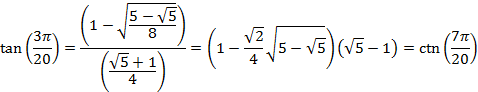
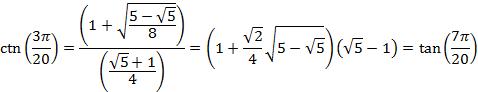
HALF-ANGLE TABLE OF VALUES