Derivative of a Logarithm
DERIVATION
We start with the function for the logarithm and calculate a change in “y” caused by a change in “x” as
![]()
![]()
![]()
where we have defined a new variable
![]()
The derivative operation for the logarithm function is
![]()
where we have defined the new variable
![]()
Recalling the binominal theorem, we can write
![]() +
+ ![]()
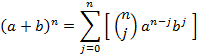
where the “binominal coefficients” are the combinatorials
![]()
noting the last expression above has “j” terms in the numerator. But in any event using this expression we can write
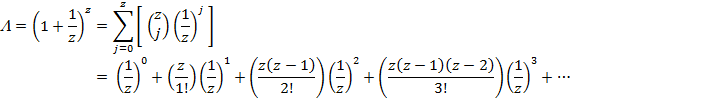
And the limit can be expressed as
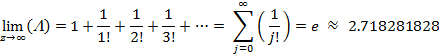
The derivative of the logarithm is thus
![]()
or for the special case of the natural logarithm
![]()
REVIEW OF LOGARITHMIC FORMULAE
A logarithm is simply an exponent. If we begin with the following expression
![]()
then we can define the logarithm as follows
![]()
In simple parlance, we say that the logarithm is that exponent which when applied to a base, yields a particular value.
A trivial result from the definition of a logarithm gives us the following
![]()
or simply
![]()
The consequences of this simple definition are several, as follows
![]()
![]()
![]()
![]()
![]()