Binominal Coefficients
INTRODUCTION
If we have the sum of two quantities raised to some power, we can immediately write the resulting polynomial without having to perform all the intermediate multiplications using the expansion as follows:
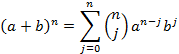
Or for example if n=5, we might write
![]()
In the above expression, the “binominal coefficients” are
the![]() terms. These are the
simple combinatorials of “n choose j” or the number of ways we can select “j”
items from a total set of “n” uniquely identifiable items. These binominal coefficients
are given by
terms. These are the
simple combinatorials of “n choose j” or the number of ways we can select “j”
items from a total set of “n” uniquely identifiable items. These binominal coefficients
are given by
![]()
For this equation, please note that both the numerator and the denominator always have “j” terms. And so for our example above for n=5, we have
![]()
![]()
![]()
![]()
![]()
And for j=0, we always define the combinatorial
![]()
PASCAL’S TRIANGLE
As an interesting side note, binominal coefficients can be easily calculated from a series of sums. To do this we construct “Pascal’s Triangle” in which each term is the sum of the two terms above it in the preceding row. For the first six rows we have
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Note that the sixth row is simply an array of the
combinatorials indicated. And please note as well, that the next line would
describe the combinatorials ![]() for j = 0, 1, …, 6.
for j = 0, 1, …, 6.